Реальная оптическая система создает изображение предмета с определенными искажениями. Отличия изображения от предмета возникают вследствие аберраций оптической системы, дифракционных явлений, дефектов изготовления и других факторов.
Характеристикой качества изображения служат аберрации различных видов в зависимости от поставленной задачи. Оптические системы с большими аберрациями характеризуют, как правило, геометрическими аберрациями, а для систем с малыми аберрациями оказывается более удобным использование волновых аберраций.
Геометрической аберрацией называется отклонение значений координат лучей, вычисленных для реальной системы, от значений координат тех же лучей, вычисленных для идеальной системы. Геометрические аберрации делят на монохроматические, которые возникают при прохождении через систему лучей света одной длины волны, и хроматические, возникающие при прохождении через систему лучей с различными длинами волн (белый свет).
К монохроматическим аберрациям относятся сферическая аберрация (продольная и поперечная), кома, астигматизм, кривизна поля и дисторсия; к хроматическим — хроматизм положения и хроматизм увеличения. Волновой аберрацией оптической системы называется отклонение реального волнового фронта от поверхности сравнения: сферы для фотографических объективов, объективов телескопов и других объективов; плоскости для телескопических систем.
Волновая аберрация выражается в единицах длин волн. Если волновая аберрация меньше или равна 0,1λ, то изображение точки можно считать идеальным. Если волновая аберрация равна 0,25λ, то изображение считают хорошим. Указанные пределы определены английским физиком Рэлеем и получили название критериев Рэлея.
Аберрации измеряют в реальных оптических системах для определения соответствия их расчетным данным и для установления влияния каждой аберрации на качество изображения. В зависимости от назначения оптической системы аберрации измеряют в угловой мере (в основном для зрительных труб и прожекторных зеркал) или в линейной (в фотографической оптике). Волновые аберрации измеряют в астрономической и микроскопической оптике для спектральных призм и т. п.
Аберрации вместе с неизбежными погрешностями изготовления оптических деталей и сборки оптических систем снижают качество изображения.
Характеристики качества изображения зависят от требований, предъявляемых к оптической системе прибора. Например, оптические системы астрономических приборов, имеющих небольшое поле и изображающих в основном бесконечно удаленные предметы, должны быть рассчитаны с минимальными аберрациями. Изображение, создаваемое такими системами, искажается вследствие дифракции. Качество изображения оптических систем, применяемых с различными приемниками (глаз, фотоматериал, электроннолучевые трубки, электронно-оптические преобразователи) и создающих изображение с большим полем, которое затем рассматривают визуально (визуальные, проекционные, фотографические, телевизионные и другие устройства), характеризуется резкостью, степенью соответствия геометрического подобия и подробностей структуры различных предметов и их изображений, а также контрастом. Оптические системы, используемые в оптико-электронных приборах для передачи световой энергии в целях дальнейшего преобразования ее в электрические сигналы, характеризуются количеством световой энергии и её распределением в изображении элементарных объектов (светящейся точки, линии).
На основании изложенного критерии оценки качества оптического изображения для различных систем выбирают в зависимости от выполняемых ими задач. Критериями оценки качества оптического изображения, адекватными перечисленным характеристикам, являются функция рассеяния, пограничная кривая и оптическая передаточная функция. Все три критерия взаимообратимы, взаимосвязаны и взаимозаменяемы, но не одинаково удобны при использовании для оценки качества изображения различных оптических систем.
Эти критерии могут быть получены из математического уравнения процесса образования оптической системой изображения, показывающего зависимость между распределением освещенности Е (х', у') в изображении и распределением яркости L (х, у) в предмете. Если предмет рассматривать как совокупность светящихся точек, то уравнение процесса образования изображения при некогерентном излучении предмета будет иметь вид
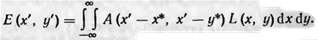(1)
Изменение распределения освещенности в плоскости изображения в указанном случае обусловливается передающими свойствами оптической системы, которые характеризуются качеством изображения бесконечно удаленной светящейся точки (при условии соблюдения изопланатичности оптической системы). Функция A(х' — х*, у' — y*) есть функция распределения освещенности изображении любой светящейся точки бесконечно удаленного предмета с координатами х, у, называемая функцией рассеяния оптической системы. Текущие координаты х*, у* точки в плоскости изображения определяют по формулам х* = βх, у* = βy, где β — линейное увеличение оптической системы. Уравнение 1 представляет собой свертку функций А и L, поэтому его можно выразить через преобразование Фурье. Тогда уравнение процесса образования изображения можно записать так:
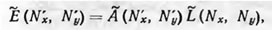(2)
где Ẽ (N'x, N'y), Ã (N'x, N’y) и Ĺ (Nx, Ny) — преобразования Фурье функций соответственно распределения освещенности в изображении Е (х', у'), рассеяния оптической системы А (х', у') и распределения яркости L (х, у) в предмете; N’x и N'y — пространственные частоты, равные обратному значению периода синусоидального изменения освещенности в пространстве изображения по двум взаимно перпендикулярным направлениям; Nx и Ny — пространственные частоты, равные обратному значению периода синусоидального изменения яркости в плоскости предмета по тем же направлениям.
Пространственные частоты в плоскости предмета и в плоскости изображения связаны зависимостью N' = βN. Уравнение 2 выражает процесс образования изображения в пространственно-частотном представлении.